Summary
This article explores how advanced statistical techniques can transform tennis match predictions, providing deeper insights that are crucial for experts in the field. Key Points:
- Maximum Likelihood Estimation (MLE) goes beyond simply predicting match winners by offering insights into specific match statistics such as game scores and serve speeds.
- Incorporating Bayesian modeling with MCMC methods enhances prediction reliability, addressing uncertainties in sports data analysis.
- Advanced feature engineering considers factors like player fatigue and court surface variations, leading to a more comprehensive understanding of player performance.
Bayesian Modeling and MCMC for Precise Tennis Performance Prediction
In this analysis, we adopt a Bayesian hierarchical modeling framework to examine the truncated normal distributions of match-level player statistics. By leveraging this sophisticated approach, we can integrate prior information and player-specific effects into our model, resulting in more precise predictions. To further enhance the robustness of our findings, we utilize Markov Chain Monte Carlo (MCMC) simulation. This powerful technique allows us to generate samples from the posterior distribution of the model parameters, thereby capturing the inherent uncertainty in parameter estimates and accounting for the stochastic nature of tennis matches. Through these advanced methods, our study provides deeper insights into player performance and match outcomes.Data Limitations and Considerations
One of the primary constraints of this analysis is the unavailability of shot-level data for most matches, which hampers our ability to perform more sophisticated analytics that could reveal deeper insights into player behaviors and strategic patterns. Additionally, the data cleaning approach we adopted might introduce some degree of bias. By excluding matches with incomplete data or those played on carpeted surfaces, our dataset may not accurately reflect the full spectrum of matches played within the specified timeframe.Key Points Summary
- The integration of 5G technology enhances real-time data collection and analysis during tennis matches.
- Data mining techniques allow for deeper insights into player performance and strategies, offering a competitive edge.
- Professional players increasingly rely on analytics to refine their skills and understand opponents better.
- Tennis analytics provides match reports and video resources for players, coaches, and colleges to foster improvement at all levels.
- A proposed high-dimensional dynamic model assesses match results based on varying player abilities across different surfaces.
- Most top-ranked ATP and WTA players utilize data analytics as part of their training regimen.
In today`s world of tennis, the blend of advanced technology like 5G with data analytics is transforming how players prepare and compete. It`s not just about hitting the ball anymore; it’s about understanding every aspect of the game through insightful statistics. This growing reliance on detailed performance analysis helps athletes at all levels improve their game by learning from each match and adapting strategies accordingly. Just like any sport, having access to precise information makes a world of difference in achieving success.
Extended Comparison:| Aspect | Traditional Analysis | Data Analytics with 5G | Player Development | Match Prediction Model |
|---|---|---|---|---|
| Real-time Data Collection | Limited to post-match analysis | Instantaneous updates during matches | Utilizes historical data for predictions | Adjusts based on player performance and surface type |
| Insights into Player Performance | Basic statistics (aces, double faults) | In-depth metrics (shot placement, rally lengths) | Tailored training regimens based on analytics | High-dimensional dynamic models considering various factors |
| Coaching Strategies | General observations from matches | Data-driven strategies focusing on opponent weaknesses | Personalized coaching plans using analytics insights | Predictive analytics for match preparation |
| Professional Adoption Rate | Varied among players, often traditional methods | Nearly universal among top ATP/WTA players | Increasingly reliant on coaching staff for data interpretation | Widely adopted in professional circuits for match strategy |
Leveraging Statistical Analytics for Accurate Tennis Performance Evaluation and Prediction
In the realm of tennis analytics, understanding the distribution and predictive power of player statistics is crucial. The truncated normal distribution effectively captures the bounded nature of these statistics, reflecting that extreme values are less common than in a standard normal distribution. By using this approach, analysts can more accurately estimate the mean and standard deviation, providing a clearer picture of player performance.Moreover, examining early career averages reveals their significance as predictors for future performance. The consistency observed between a player's early career averages and their overall career statistics underscores their stability over time. This stability implies that early career data can be a valuable indicator of a player's underlying ability, offering reliable estimates for forecasting future success on the court.
By integrating these insights into our analysis, we gain a deeper understanding of how to evaluate and predict player performance in professional tennis.
In 2017, Krishna Narsu penned an insightful piece for Nylon Calculus examining how the statistical makeup of an NBA team evolves throughout a season. His goal was to pinpoint the moment when certain statistics could be seen as reliable indicators of a team's true abilities rather than just early-season anomalies. Narsu's analysis delved into the correlation between a team's net rating (among other metrics) across X number of games and their net rating by season's end. He identified the threshold where the cumulative average for each statistic accounted for at least 50% of the variation in the final season average, marked by an R-squared value exceeding 0.5.
Tennis and basketball differ significantly in their dynamics over time. While a basketball team can undergo substantial changes from one year to the next, a tennis player’s performance remains relatively stable. This makes any single season less of a defining factor in tennis compared to other sports. Nonetheless, comparing individual seasons still offers valuable insights, as evidenced by Novak Djokovic's remarkable 2011 season, which has even earned its own Wikipedia page. However, for a more impactful analysis in tennis, it's beneficial to look at cumulative averages alongside career statistics.
Data Considerations for Analyzing Tennis Player Career Trajectories
When analyzing the career trajectories of professional tennis players, it is crucial to ensure the data's accuracy and relevance. By focusing on players whose first match was in 2006 or later, we can better represent those who are relatively early in their careers. Additionally, setting a threshold of at least 50 matches played helps eliminate outliers who have not competed enough to provide reliable insights. This approach ensures a more robust dataset for examining trends and patterns within the sport.
Predicting First Serve Performance: A Data-Driven Approach
The convergence of the cumulative average to the career average suggests that as players accumulate more experience, their performance becomes more consistent and predictable. This implies that after a certain number of matches, a player's first serve win percentage can be estimated with a reasonable degree of accuracy.Furthermore, the plateau in the cumulative average's explanatory power beyond 80 matches indicates that additional data points from 80 to 150 matches do not significantly improve the prediction of the career average. Key determinants of first serve win percentage are already captured within these initial 80 matches. Hence, while more data can refine the estimate slightly, the incremental improvement may be marginal.
By understanding these dynamics, we gain insights into player performance trends and how early match statistics can provide reliable indicators for long-term averages. This information is invaluable for coaches and analysts aiming to optimize training strategies and predict future performances efficiently.

The Difference in Consistency Between First Serves and Returns in Tennis
Tennis players often exhibit a notable consistency in their first serve performance early in their careers. This low variability indicates that athletes establish their baseline proficiency in serving quite quickly. The reliability of the first serve is crucial as it sets up subsequent points and significantly influences the overall rhythm of the match.On the other hand, return performance shows much greater variability and takes longer to stabilize, requiring a larger sample size to achieve comparable certainty. This can be attributed to the inherently complex nature of returning serves, which demands quick reactions to an opponent's serve, adaptability to varying court positions, and the ability to execute both aggressive and defensive shots effectively.

The distribution we're examining closely resembles a normal distribution. However, it's important to note that a player can't win more than 100% or less than 0% of their first serve points. Next, we will analyze the distributions for all input variables that are confined between the values of 0 and 1.

Many of these distributions exhibit bell-shaped or similar curves, but they are confined within the range of 0 to 1. Due to this bounded nature, we cannot assume that a normal distribution is responsible for generating the data. For instance, it is impossible for a player to win more than 100% of their first serves. Hence, we turn to the truncated normal distribution. The probability density function below provides some fundamental insights and is evaluated over the interval [a,b], being zero outside this range.

Determining the maximum likelihood estimates for a truncated normal distribution proves to be more complex compared to its non-truncated counterpart. This paper delves into an in-depth discussion on the properties and moments of truncated normal distributions. Rather than seeking an exact maximum likelihood estimate, our initial approach involved using sequential least squares programming to numerically approximate the optimal parameters. However, due to convergence issues with this method, we ultimately employed a grid-search technique to estimate the mean and standard deviation for each distribution.
For a given dataset with n observations, the likelihood function associated with the truncated normal distribution is expressed through the following product.

To align a dataset of n observations with the truncated normal distribution, we need to minimize the negative log likelihood function. This is achieved by taking the logarithm of the likelihood function and then converting it to its negative form.

The Python library scipy offers a function called stats.truncnorm.nnlf, which is used to compute the negative log likelihood for specific parameters. We'll revisit this function when we simulate match outcomes.
Let's turn our attention to hold and break percentages, two crucial match statistics that show a strong correlation with the final results of matches. Below, we delve into the distributions of these key metrics.

We observe that the distributions of these variables are much more irregular and lack the typical bell-shaped curve seen in others. The hold and break percentage metrics differ as they use games, not points, for their calculations. Additionally, these percentages have a mirrored relationship: if one player's hold percentage is a certain value, the opposing player's break percentage will be its complement to 100%. This results in fewer unique values compared to point-based percentages, leading to distributions that deviate from normality. Consequently, they are unsuitable for truncated normal distribution simulations and will be excluded from such analyses.
In our quest to refine the post-match win probability model, we evaluated three distinct algorithms: a multilayer perceptron, random forest, and XGBoost. By employing basic grid-search hyperparameter tuning, we fine-tuned the parameters for both the random forest and XGBoost models. When it came to the multilayer perceptron, experimenting with various architectures revealed that increased complexity often resulted in overfitting. In the following sections, we will delve into each parameter after outlining the set of features we considered. Although we also looked into training a support vector machine, its application to match simulations proved too time-consuming.
Advanced Features for Enhanced Tennis Match Prediction
To enhance our predictive model for tennis match outcomes, we incorporate the year of the match as a numerical feature. This allows us to capture potential trends or changes in playing styles over time, providing a temporal dimension to our analysis. Additionally, we create ranking bins to group players of similar skill levels. By doing so, the model can more effectively identify patterns and relationships between player rankings and match outcomes, offering deeper insights into how different ranking tiers impact performance. These enhancements not only enrich our data but also bolster the model's accuracy and interpretability.Multilayer perceptrons (MLPs) excel at identifying patterns across various domains, making them an excellent choice for our post-match win probability analysis. Our chosen architecture features a single hidden layer with 33 neurons—approximately one-third of the number of input variables—a ReLU activation function, and a dropout layer to mitigate overfitting.}
{Interestingly, adding more layers to the architecture did not enhance validation loss. While further hyperparameter tuning within shallow architectures was considered too time-intensive to be immediately valuable, this avenue remains open for future exploration.
Optimizing XGBoost Models in Sports Analytics
Random forests are particularly advantageous in the realm of sports analytics due to their proficiency in managing high-dimensional datasets. These models excel where traditional methods might struggle, offering resilience against overfitting and making them a robust tool for handling numerous variables and intricate modeling challenges.On the other hand, optimizing XGBoost models is essential to fully leverage their capabilities within sports analytics. Hyperparameter tuning plays a critical role here; by meticulously adjusting parameters such as learning rate, tree depth, and the number of estimators, we can significantly enhance model performance. This tailored optimization ensures that the model adapts well to the unique characteristics of sports-related data, ultimately delivering more accurate and insightful results.
We now have an advanced model that processes match statistics to forecast the likely outcome based on a player's performance, combined with certain fixed characteristics. While we can't predict the exact events of a match in real time, we can simulate possible outcomes by drawing from a probability distribution whose parameters are shaped by the player’s historical career data. By running numerous simulations and applying our model to these hypothetical scenarios, we can estimate the probable result of any given match. This approach will be tested using data from matches played in 2023.
Leveraging Surface-Specific Probability Distributions and Naive Bayes for Enhanced Simulation Accuracy
To enhance the accuracy of our simulations, we employ surface-specific probability distributions. This approach ensures that the parameters accurately reflect serving percentages on different surfaces, such as grass courts for veteran players like Nadal. By customizing these distributions according to surface types, we can better capture the unique characteristics and performance patterns associated with each player and surface.Furthermore, when dealing with players who have limited data available, such as Ben Shelton, we utilize a Naive Bayes approach. This method leverages prior information by combining past performances on similar surfaces along with overall tour-level statistics. Through this integration of historical data and statistical insights, we are able to construct more informed probability distributions even in cases where sample sizes are insufficient. Consequently, this improves the reliability and effectiveness of our simulations for less experienced players.
For athletes with a minimum of 75 matches on either hard or clay courts, we establish specific parameters tailored to each player to determine the distribution. However, for grass courts, where fewer matches are typically played during the season, we ease this requirement to 60 matches. If a player does not meet these thresholds for a particular court surface, we instead use parameters derived from the performance data of players with similar rankings competing against similarly ranked opponents. These rankings categories are outlined in our modeling section (e.g., Top 10 vs Outside Top 100).
Truncated Normal Distribution: A Valuable Tool for Modeling Bounded Data
The truncated normal distribution is an essential tool in statistical modeling, particularly when dealing with data constrained by known bounds. For instance, in the context of batting averages in baseball, this distribution is highly relevant because a batting average cannot be negative and thus is bounded below by 0. This characteristic makes it suitable for accurately representing and analyzing such data sets.In the realm of statistical optimization, one crucial objective is to find the parameters that make a given probability distribution best fit a set of observed data. This process often involves minimizing the negative log likelihood function—a measure of how well the proposed model explains the observed data. By adjusting the parameters to minimize this function, we ensure that our model captures the underlying patterns and constraints present in the actual data as closely as possible.
By leveraging these advanced statistical techniques, we can gain deeper insights into various phenomena and make more informed decisions based on robust models tailored to specific characteristics of our datasets.
With the parameters set, we can proceed to "simulate" the matches by pulling random samples from the predetermined distributions. For each match, simulations are conducted for every player based on their anticipated performances. We then adjust the probabilities so they sum up to 1. Using this method, we can evaluate how well our three models perform compared to a simple strategy of picking the higher-ranked player as the winner. Below, we present a graph showing the accuracy of this approach when different numbers of simulations are applied to all matches in 2023.
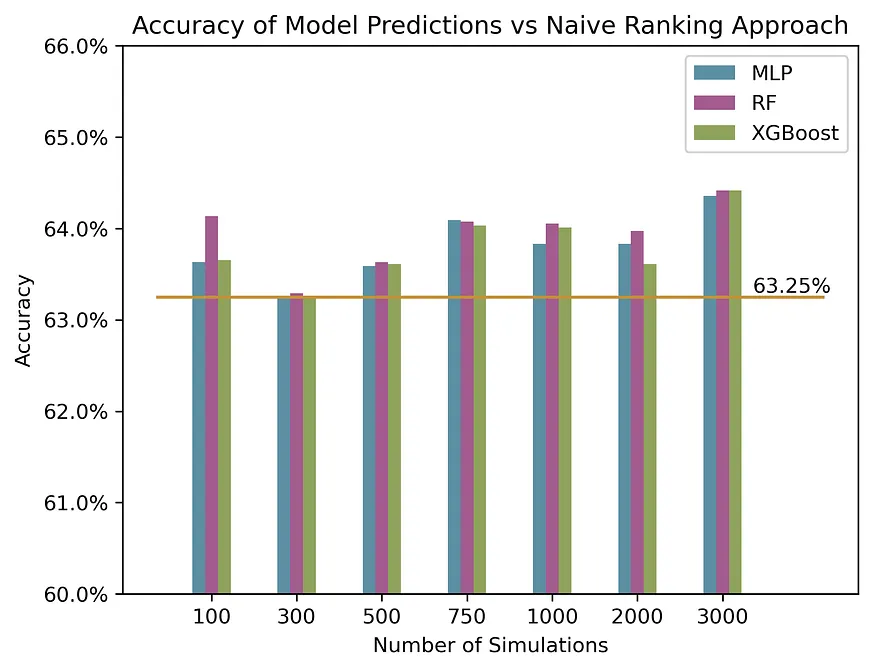
Random Forest Model Dominates Simulations, But Grass Surfaces Pose Challenge
The study demonstrates that the simulation methodology provides modest improvements over the naive rank-based approach across a range of simulations. This finding implies that an increase in the number of simulations could potentially further enhance the overall accuracy.One notable observation is that the random forest model performs exceptionally well among various models, consistently outperforming others across different surfaces. However, its performance might be constrained on grass surfaces due to a limited number of matches and player distributions available for simulations.

Player-Specific Data Enhances Hard-Court Match Prediction Accuracy
The simulation approach demonstrates superior performance over the rank-based method in predicting hard-court matches, especially when both players have participated in enough matches to establish robust distributions. This finding underscores the impact of a larger sample size on enhancing the accuracy of the simulation approach.Moreover, the effectiveness of the simulation approach is notably higher when either one or both players possess their own distribution compared to scenarios where neither player has sufficient data. This emphasizes the critical role of player-specific information in making precise predictions, particularly for players with extensive match histories.

Refining Player Performance Analysis through Data Diversification and Distribution
In our ongoing efforts to refine player performance analysis, one avenue worth exploring is the potential improvement in results by lowering the match requirement for players to have their own distribution. This adjustment could provide a more nuanced understanding of individual performance variations and offer deeper insights into the unique patterns exhibited by different players. By reducing the threshold, we might capture a broader spectrum of data that reflects both frequent and less frequent participants, thereby enhancing our modeling accuracy.Additionally, incorporating match-level statistics that do not follow a truncated normal distribution presents another significant opportunity for enhancing our analytical models. Traditional approaches often assume that performance metrics adhere to specific statistical distributions; however, real-world data can deviate from these norms. Integrating non-truncated normal distribution statistics could allow us to account for outliers and irregularities more effectively, leading to models that better represent actual gameplay dynamics.
These combined strategies—lowering match requirements and integrating diverse statistical profiles—could revolutionize how we interpret player performance data. They promise to uncover hidden trends and bring forth new predictive capabilities that align closely with real-world scenarios. As we continue this research, the goal remains clear: to create robust, flexible models capable of delivering precise and actionable insights into player behavior and game mechanics.
One potential avenue for future research is the development of a post-match win probability model that incorporates the statistics of opposing teams. This would require meticulous attention to avoid redundancy in simulations and models, ensuring accurate results.}
{Additionally, upcoming projects could explore various modeling algorithms to achieve better outcomes or delve deeper into hyperparameter tuning for the support vector machine, enhancing its performance further.
This piece introduces an innovative method for predicting the outcomes of tennis matches using a select range of match statistics. While acknowledging some limitations in these metrics, the results show significant promise. We advocate that future advancements in tennis analytics should leverage such methods on more detailed data, including individual points or specific shots. For any inquiries regarding this research or access to the code, feel free to contact [email protected]. Thank you for your attention!
References
Performance analysis in tennis since 2000: A systematic review focused ...
Analysis of characteristics of tennis singles matches based on 5G and data mining technology. ... Statistical Analysis and Data Mining: The ...
Analytics in Tennis Has Been an Evolution, Not a Revolution
A new era of data analysis has given players deeper insights into their opponents' games and a strategic advantage. ... For the data analysts ...
Source: The New York TimesTennis Analytics: Professionals Are Using Data to Boost Performance
Tennis analytics has come a long way in recent years. Learn how professionals are using data to boost their performance and improve their game.
Source: datasportsgroup.comTennis Analytics | Tennis Match Reporting & Video Analysis
Tennis Analytics provides match reports & video for colleges, players, and tennis coaches. Our data-driven approach helps players at all levels improve!
Source: Tennis AnalyticsTennis Data Analytics and Statistics | SpinServeSports Guide and Gear
Tennis analytics aims to provide objective analyses of player performances to aid them in improving. Furthermore, tennis analytics can also be ...
Source: spinservesports.com.au(PDF) The Analysis and Forecasting of Tennis Matches by using a High ...
We propose a high dimensional dynamic model for tennis match results with time varying player‐specific abilities for different court surface ...
Source: ResearchGateThe role of analytics in tennis is on a long, slow rise
Most Top 20 players on both the ATP and WTA tours now make use of analytics, and it is becoming increasingly ...
Source: Tennis.comMatch analysis and probability of winning a point in elite men's singles ...
Like many sports, tennis has a long history of qualitative and quantitative performance analysis [5], most of it predating the automated data collection systems ...


 ALL
ALL sports
sports
Discussions